Mathematics of imaging the black hole The 2019 Stack Overflow Developer Survey Results Are In Unicorn Meta Zoo #1: Why another podcast? Announcing the arrival of Valued Associate #679: Cesar ManaraEstimating the derivative of a noisy, non-uniformly sampled functionMathematics TV clipsSwitching from pure mathematics (e.g. geometry) to more applied areas (e.g imaging) after Ph.D., as postdoc and chance of getting such a postdoc?Choosing the order of Tikhonov regularization of an inverse problemSample based inversion of the Radon transformWhen is a mapping the proximity operator of some convex function?The jump set of $SBV$ function for different value of parameter in image denoising problemCan the wavelet bispectrum be normalised so that its integral “gives the right answer”?Is there any paper which summarizes the mathematical foundation of deep learning?Strategies to make the sum operation bijective in a contribution problem
Mathematics of imaging the black hole
The 2019 Stack Overflow Developer Survey Results Are In
Unicorn Meta Zoo #1: Why another podcast?
Announcing the arrival of Valued Associate #679: Cesar ManaraEstimating the derivative of a noisy, non-uniformly sampled functionMathematics TV clipsSwitching from pure mathematics (e.g. geometry) to more applied areas (e.g imaging) after Ph.D., as postdoc and chance of getting such a postdoc?Choosing the order of Tikhonov regularization of an inverse problemSample based inversion of the Radon transformWhen is a mapping the proximity operator of some convex function?The jump set of $SBV$ function for different value of parameter in image denoising problemCan the wavelet bispectrum be normalised so that its integral “gives the right answer”?Is there any paper which summarizes the mathematical foundation of deep learning?Strategies to make the sum operation bijective in a contribution problem
$begingroup$
The first ever black hole was "pictured" recently, per an announcement made on 10th April, 2019. See for example: https://www.bbc.com/news/science-environment-47873592 .
It has been claimed that state-of-the-art imaging algorithms were an enabler for this historic success. Does anybody care to describe the difficulties, and (quite certainly non-trivial) mathematics that went into this effort ?
signal-analysis inverse-problems machine-learning image-processing popularization
edited yesterday
Rodrigo de Azevedo
1,8422820
asked 2 days ago
Piyush GroverPiyush Grover
1,63511328
$endgroup$
add a comment |
$begingroup$
The first ever black hole was "pictured" recently, per an announcement made on 10th April, 2019. See for example: https://www.bbc.com/news/science-environment-47873592 .
It has been claimed that state-of-the-art imaging algorithms were an enabler for this historic success. Does anybody care to describe the difficulties, and (quite certainly non-trivial) mathematics that went into this effort ?
signal-analysis inverse-problems machine-learning image-processing popularization
edited yesterday
Rodrigo de Azevedo
1,8422820
asked 2 days ago
Piyush GroverPiyush Grover
1,63511328
$endgroup$
7
$begingroup$
For reference here is the paper where the collaboration described data processing: iopscience.iop.org/article/10.3847/2041-8213/ab0c57/meta
$endgroup$
– Neal
2 days ago
$begingroup$
Katie Bouman's work might shed some light here!
$endgroup$
– yousuf soliman
2 days ago
3
$begingroup$
But, @yousuf, will that light be able to escape from the black hole?
$endgroup$
– Gerry Myerson
yesterday
5
$begingroup$
The actual image reconstruction is described in paper IV: iopscience.iop.org/article/10.3847/2041-8213/ab0e85. In a nutshell, they formulated a baker's dozen of data misfit (for all the different acquired data as described in paper III) and regularization (including total variation and sparsity) functionals, and then minimized their weighted sum using L-BFGS. Not quite state-of-the-art from a mathematical point of view (especially using BFGS for a non-differentiable functional), but close enough.
$endgroup$
– Christian Clason
yesterday
4
$begingroup$
Great post and answer. For those also interested on the physics side of the discussions, here's a recent post: physics.stackexchange.com/questions/471972/…
$endgroup$
– user929304
yesterday
add a comment |
$begingroup$
The first ever black hole was "pictured" recently, per an announcement made on 10th April, 2019. See for example: https://www.bbc.com/news/science-environment-47873592 .
It has been claimed that state-of-the-art imaging algorithms were an enabler for this historic success. Does anybody care to describe the difficulties, and (quite certainly non-trivial) mathematics that went into this effort ?
signal-analysis inverse-problems machine-learning image-processing popularization
edited yesterday
Rodrigo de Azevedo
1,8422820
asked 2 days ago
Piyush GroverPiyush Grover
1,63511328
$endgroup$
The first ever black hole was "pictured" recently, per an announcement made on 10th April, 2019. See for example: https://www.bbc.com/news/science-environment-47873592 .
It has been claimed that state-of-the-art imaging algorithms were an enabler for this historic success. Does anybody care to describe the difficulties, and (quite certainly non-trivial) mathematics that went into this effort ?
signal-analysis inverse-problems machine-learning image-processing popularization
signal-analysis inverse-problems machine-learning image-processing popularization
edited yesterday
Rodrigo de Azevedo
1,8422820
asked 2 days ago
Piyush GroverPiyush Grover
1,63511328
edited yesterday
Rodrigo de Azevedo
1,8422820
asked 2 days ago
Piyush GroverPiyush Grover
1,63511328
edited yesterday
Rodrigo de Azevedo
1,8422820
edited yesterday
Rodrigo de Azevedo
1,8422820
edited yesterday
Rodrigo de Azevedo
1,8422820
1,8422820
asked 2 days ago
Piyush GroverPiyush Grover
1,63511328
asked 2 days ago
Piyush GroverPiyush Grover
1,63511328
asked 2 days ago
Piyush GroverPiyush Grover
1,63511328
1,63511328
7
$begingroup$
For reference here is the paper where the collaboration described data processing: iopscience.iop.org/article/10.3847/2041-8213/ab0c57/meta
$endgroup$
– Neal
2 days ago
$begingroup$
Katie Bouman's work might shed some light here!
$endgroup$
– yousuf soliman
2 days ago
3
$begingroup$
But, @yousuf, will that light be able to escape from the black hole?
$endgroup$
– Gerry Myerson
yesterday
5
$begingroup$
The actual image reconstruction is described in paper IV: iopscience.iop.org/article/10.3847/2041-8213/ab0e85. In a nutshell, they formulated a baker's dozen of data misfit (for all the different acquired data as described in paper III) and regularization (including total variation and sparsity) functionals, and then minimized their weighted sum using L-BFGS. Not quite state-of-the-art from a mathematical point of view (especially using BFGS for a non-differentiable functional), but close enough.
$endgroup$
– Christian Clason
yesterday
4
$begingroup$
Great post and answer. For those also interested on the physics side of the discussions, here's a recent post: physics.stackexchange.com/questions/471972/…
$endgroup$
– user929304
yesterday
add a comment |
7
$begingroup$
For reference here is the paper where the collaboration described data processing: iopscience.iop.org/article/10.3847/2041-8213/ab0c57/meta
$endgroup$
– Neal
2 days ago
$begingroup$
Katie Bouman's work might shed some light here!
$endgroup$
– yousuf soliman
2 days ago
3
$begingroup$
But, @yousuf, will that light be able to escape from the black hole?
$endgroup$
– Gerry Myerson
yesterday
5
$begingroup$
The actual image reconstruction is described in paper IV: iopscience.iop.org/article/10.3847/2041-8213/ab0e85. In a nutshell, they formulated a baker's dozen of data misfit (for all the different acquired data as described in paper III) and regularization (including total variation and sparsity) functionals, and then minimized their weighted sum using L-BFGS. Not quite state-of-the-art from a mathematical point of view (especially using BFGS for a non-differentiable functional), but close enough.
$endgroup$
– Christian Clason
yesterday
4
$begingroup$
Great post and answer. For those also interested on the physics side of the discussions, here's a recent post: physics.stackexchange.com/questions/471972/…
$endgroup$
– user929304
yesterday
7
7
$begingroup$
For reference here is the paper where the collaboration described data processing: iopscience.iop.org/article/10.3847/2041-8213/ab0c57/meta
$endgroup$
– Neal
2 days ago
$begingroup$
For reference here is the paper where the collaboration described data processing: iopscience.iop.org/article/10.3847/2041-8213/ab0c57/meta
$endgroup$
– Neal
2 days ago
$begingroup$
Katie Bouman's work might shed some light here!
$endgroup$
– yousuf soliman
2 days ago
$begingroup$
Katie Bouman's work might shed some light here!
$endgroup$
– yousuf soliman
2 days ago
3
3
$begingroup$
But, @yousuf, will that light be able to escape from the black hole?
$endgroup$
– Gerry Myerson
yesterday
$begingroup$
But, @yousuf, will that light be able to escape from the black hole?
$endgroup$
– Gerry Myerson
yesterday
5
5
$begingroup$
The actual image reconstruction is described in paper IV: iopscience.iop.org/article/10.3847/2041-8213/ab0e85. In a nutshell, they formulated a baker's dozen of data misfit (for all the different acquired data as described in paper III) and regularization (including total variation and sparsity) functionals, and then minimized their weighted sum using L-BFGS. Not quite state-of-the-art from a mathematical point of view (especially using BFGS for a non-differentiable functional), but close enough.
$endgroup$
– Christian Clason
yesterday
$begingroup$
The actual image reconstruction is described in paper IV: iopscience.iop.org/article/10.3847/2041-8213/ab0e85. In a nutshell, they formulated a baker's dozen of data misfit (for all the different acquired data as described in paper III) and regularization (including total variation and sparsity) functionals, and then minimized their weighted sum using L-BFGS. Not quite state-of-the-art from a mathematical point of view (especially using BFGS for a non-differentiable functional), but close enough.
$endgroup$
– Christian Clason
yesterday
4
4
$begingroup$
Great post and answer. For those also interested on the physics side of the discussions, here's a recent post: physics.stackexchange.com/questions/471972/…
$endgroup$
– user929304
yesterday
$begingroup$
Great post and answer. For those also interested on the physics side of the discussions, here's a recent post: physics.stackexchange.com/questions/471972/…
$endgroup$
– user929304
yesterday
add a comment |
1 Answer
1
active
oldest
votes
$begingroup$
Essential elements of the reconstruction algorithm were developed at MIT under the name CHIRP = Continuous High-resolution Image Reconstruction using Patch priors, as described in Computational Imaging for VLBI Image Reconstruction (2015).
The difficulty of VLBI (Very Long Baseline Interferometry Image) reconstruction is that the inversion problem is highly-ill posed, there are many images that explain the data. The challenge is to find an explanation that respects our prior assumptions about the “visual” universe while still satisfying the observed data. Bayesian approaches are generally employed for that purpose, in CHIRP machine learning is used to automatically identify visual patterns --- obviating the need for hand training of the algorithm.
A key technical innovation is a way to correct for the delays in the signal received from the various telescopes. The delays are difficult to predict, since they depend the local variations in the speed of the radio waves through the noisy atmosphere. CHIRP adopts an algebraic solution known as phase closure to this problem: If the measurements from three telescopes are multiplied, the extra delays caused by atmospheric noise cancel each other out.
One test case that shows the resolving power of CHIRP, compared to a competing algorithm (BU) is shown below (taken from the MIT paper). Notice how CHIRP is able to resolve 2 separate, previously unresolved, bright emissions in the blazar OJ287.
answered yesterday
Carlo BeenakkerCarlo Beenakker
80.4k9193295
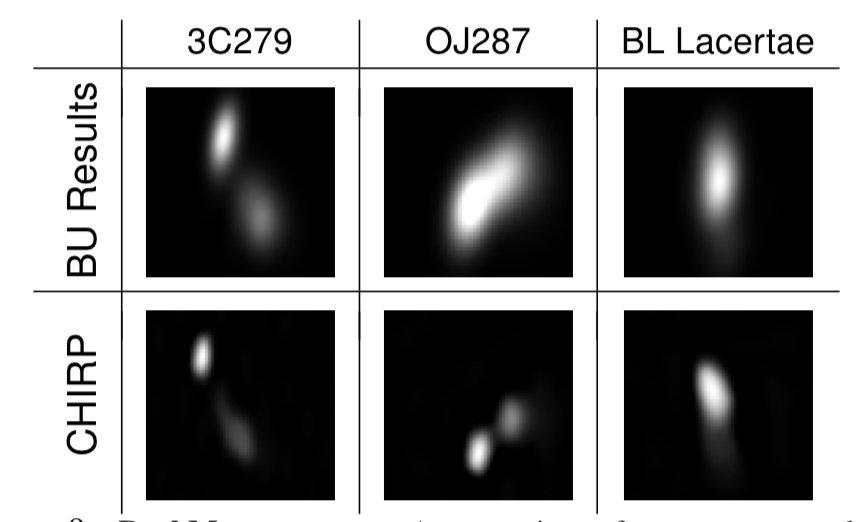
$endgroup$
add a comment |
Your Answer
StackExchange.ready(function()
var channelOptions =
tags: "".split(" "),
id: "504"
;
initTagRenderer("".split(" "), "".split(" "), channelOptions);
StackExchange.using("externalEditor", function()
// Have to fire editor after snippets, if snippets enabled
if (StackExchange.settings.snippets.snippetsEnabled)
StackExchange.using("snippets", function()
createEditor();
);
else
createEditor();
);
function createEditor()
StackExchange.prepareEditor(
heartbeatType: 'answer',
autoActivateHeartbeat: false,
convertImagesToLinks: true,
noModals: true,
showLowRepImageUploadWarning: true,
reputationToPostImages: 10,
bindNavPrevention: true,
postfix: "",
imageUploader:
brandingHtml: "Powered by u003ca class="icon-imgur-white" href="https://imgur.com/"u003eu003c/au003e",
contentPolicyHtml: "User contributions licensed under u003ca href="https://creativecommons.org/licenses/by-sa/3.0/"u003ecc by-sa 3.0 with attribution requiredu003c/au003e u003ca href="https://stackoverflow.com/legal/content-policy"u003e(content policy)u003c/au003e",
allowUrls: true
,
noCode: true, onDemand: true,
discardSelector: ".discard-answer"
,immediatelyShowMarkdownHelp:true
);
);
Sign up or log in
StackExchange.ready(function ()
StackExchange.helpers.onClickDraftSave('#login-link');
);
Sign up using Google
Sign up using Facebook
Sign up using Email and Password
Post as a guest
Required, but never shown
StackExchange.ready(
function ()
StackExchange.openid.initPostLogin('.new-post-login', 'https%3a%2f%2fmathoverflow.net%2fquestions%2f327733%2fmathematics-of-imaging-the-black-hole%23new-answer', 'question_page');
);
Post as a guest
Required, but never shown
1 Answer
1
active
oldest
votes
1 Answer
1
active
oldest
votes
active
oldest
votes
active
oldest
votes
$begingroup$
Essential elements of the reconstruction algorithm were developed at MIT under the name CHIRP = Continuous High-resolution Image Reconstruction using Patch priors, as described in Computational Imaging for VLBI Image Reconstruction (2015).
The difficulty of VLBI (Very Long Baseline Interferometry Image) reconstruction is that the inversion problem is highly-ill posed, there are many images that explain the data. The challenge is to find an explanation that respects our prior assumptions about the “visual” universe while still satisfying the observed data. Bayesian approaches are generally employed for that purpose, in CHIRP machine learning is used to automatically identify visual patterns --- obviating the need for hand training of the algorithm.
A key technical innovation is a way to correct for the delays in the signal received from the various telescopes. The delays are difficult to predict, since they depend the local variations in the speed of the radio waves through the noisy atmosphere. CHIRP adopts an algebraic solution known as phase closure to this problem: If the measurements from three telescopes are multiplied, the extra delays caused by atmospheric noise cancel each other out.
One test case that shows the resolving power of CHIRP, compared to a competing algorithm (BU) is shown below (taken from the MIT paper). Notice how CHIRP is able to resolve 2 separate, previously unresolved, bright emissions in the blazar OJ287.
answered yesterday
Carlo BeenakkerCarlo Beenakker
80.4k9193295
$endgroup$
add a comment |
$begingroup$
Essential elements of the reconstruction algorithm were developed at MIT under the name CHIRP = Continuous High-resolution Image Reconstruction using Patch priors, as described in Computational Imaging for VLBI Image Reconstruction (2015).
The difficulty of VLBI (Very Long Baseline Interferometry Image) reconstruction is that the inversion problem is highly-ill posed, there are many images that explain the data. The challenge is to find an explanation that respects our prior assumptions about the “visual” universe while still satisfying the observed data. Bayesian approaches are generally employed for that purpose, in CHIRP machine learning is used to automatically identify visual patterns --- obviating the need for hand training of the algorithm.
A key technical innovation is a way to correct for the delays in the signal received from the various telescopes. The delays are difficult to predict, since they depend the local variations in the speed of the radio waves through the noisy atmosphere. CHIRP adopts an algebraic solution known as phase closure to this problem: If the measurements from three telescopes are multiplied, the extra delays caused by atmospheric noise cancel each other out.
One test case that shows the resolving power of CHIRP, compared to a competing algorithm (BU) is shown below (taken from the MIT paper). Notice how CHIRP is able to resolve 2 separate, previously unresolved, bright emissions in the blazar OJ287.
answered yesterday
Carlo BeenakkerCarlo Beenakker
80.4k9193295
$endgroup$
add a comment |
$begingroup$
Essential elements of the reconstruction algorithm were developed at MIT under the name CHIRP = Continuous High-resolution Image Reconstruction using Patch priors, as described in Computational Imaging for VLBI Image Reconstruction (2015).
The difficulty of VLBI (Very Long Baseline Interferometry Image) reconstruction is that the inversion problem is highly-ill posed, there are many images that explain the data. The challenge is to find an explanation that respects our prior assumptions about the “visual” universe while still satisfying the observed data. Bayesian approaches are generally employed for that purpose, in CHIRP machine learning is used to automatically identify visual patterns --- obviating the need for hand training of the algorithm.
A key technical innovation is a way to correct for the delays in the signal received from the various telescopes. The delays are difficult to predict, since they depend the local variations in the speed of the radio waves through the noisy atmosphere. CHIRP adopts an algebraic solution known as phase closure to this problem: If the measurements from three telescopes are multiplied, the extra delays caused by atmospheric noise cancel each other out.
One test case that shows the resolving power of CHIRP, compared to a competing algorithm (BU) is shown below (taken from the MIT paper). Notice how CHIRP is able to resolve 2 separate, previously unresolved, bright emissions in the blazar OJ287.
answered yesterday
Carlo BeenakkerCarlo Beenakker
80.4k9193295
$endgroup$
Essential elements of the reconstruction algorithm were developed at MIT under the name CHIRP = Continuous High-resolution Image Reconstruction using Patch priors, as described in Computational Imaging for VLBI Image Reconstruction (2015).
The difficulty of VLBI (Very Long Baseline Interferometry Image) reconstruction is that the inversion problem is highly-ill posed, there are many images that explain the data. The challenge is to find an explanation that respects our prior assumptions about the “visual” universe while still satisfying the observed data. Bayesian approaches are generally employed for that purpose, in CHIRP machine learning is used to automatically identify visual patterns --- obviating the need for hand training of the algorithm.
A key technical innovation is a way to correct for the delays in the signal received from the various telescopes. The delays are difficult to predict, since they depend the local variations in the speed of the radio waves through the noisy atmosphere. CHIRP adopts an algebraic solution known as phase closure to this problem: If the measurements from three telescopes are multiplied, the extra delays caused by atmospheric noise cancel each other out.
One test case that shows the resolving power of CHIRP, compared to a competing algorithm (BU) is shown below (taken from the MIT paper). Notice how CHIRP is able to resolve 2 separate, previously unresolved, bright emissions in the blazar OJ287.
answered yesterday
Carlo BeenakkerCarlo Beenakker
80.4k9193295
edited yesterday
answered yesterday
Carlo BeenakkerCarlo Beenakker
80.4k9193295
answered yesterday
Carlo BeenakkerCarlo Beenakker
80.4k9193295
answered yesterday
Carlo BeenakkerCarlo Beenakker
80.4k9193295
80.4k9193295
add a comment |
add a comment |
Thanks for contributing an answer to MathOverflow!
- Please be sure to answer the question. Provide details and share your research!
But avoid …
- Asking for help, clarification, or responding to other answers.
- Making statements based on opinion; back them up with references or personal experience.
Use MathJax to format equations. MathJax reference.
To learn more, see our tips on writing great answers.
Sign up or log in
StackExchange.ready(function ()
StackExchange.helpers.onClickDraftSave('#login-link');
);
Sign up using Google
Sign up using Facebook
Sign up using Email and Password
Post as a guest
Required, but never shown
StackExchange.ready(
function ()
StackExchange.openid.initPostLogin('.new-post-login', 'https%3a%2f%2fmathoverflow.net%2fquestions%2f327733%2fmathematics-of-imaging-the-black-hole%23new-answer', 'question_page');
);
Post as a guest
Required, but never shown
Sign up or log in
StackExchange.ready(function ()
StackExchange.helpers.onClickDraftSave('#login-link');
);
Sign up using Google
Sign up using Facebook
Sign up using Email and Password
Post as a guest
Required, but never shown
Sign up or log in
StackExchange.ready(function ()
StackExchange.helpers.onClickDraftSave('#login-link');
);
Sign up using Google
Sign up using Facebook
Sign up using Email and Password
Post as a guest
Required, but never shown
Sign up or log in
StackExchange.ready(function ()
StackExchange.helpers.onClickDraftSave('#login-link');
);
Sign up using Google
Sign up using Facebook
Sign up using Email and Password
Sign up using Google
Sign up using Facebook
Sign up using Email and Password
Post as a guest
Required, but never shown
Required, but never shown
Required, but never shown
Required, but never shown
Required, but never shown
Required, but never shown
Required, but never shown
Required, but never shown
Required, but never shown
7
$begingroup$
For reference here is the paper where the collaboration described data processing: iopscience.iop.org/article/10.3847/2041-8213/ab0c57/meta
$endgroup$
– Neal
2 days ago
$begingroup$
Katie Bouman's work might shed some light here!
$endgroup$
– yousuf soliman
2 days ago
3
$begingroup$
But, @yousuf, will that light be able to escape from the black hole?
$endgroup$
– Gerry Myerson
yesterday
5
$begingroup$
The actual image reconstruction is described in paper IV: iopscience.iop.org/article/10.3847/2041-8213/ab0e85. In a nutshell, they formulated a baker's dozen of data misfit (for all the different acquired data as described in paper III) and regularization (including total variation and sparsity) functionals, and then minimized their weighted sum using L-BFGS. Not quite state-of-the-art from a mathematical point of view (especially using BFGS for a non-differentiable functional), but close enough.
$endgroup$
– Christian Clason
yesterday
4
$begingroup$
Great post and answer. For those also interested on the physics side of the discussions, here's a recent post: physics.stackexchange.com/questions/471972/…
$endgroup$
– user929304
yesterday